Number System

There are basically 4 type of number systems based on number of digits. Every number system has a unique base depending on the number of digits such as a decimal number system has base 10, as it has a total of 10 digits (0-9). A hexadecimal number system has base 16 as it has 16 digits where first 10 digits are same as in decimal number system (0 to 9) and for rest of 6 digits, alphabets are allotted, where 10 is represented by 'A', 11 by 'B', similarly 15 by 'F'.

The way to store a number of any number system is to enclose the number in ( ) with its base at the bottom right of closing brace.

example: (75)10 , ( 1001011)2 , (113 )8 , ( 42B)16

Following are the number systems we will study.

1) Decimal Number System (Digits 0 to 9, Base :10)

2) Binary Number System (Digits 0 & 1, Base :2)

3) Octal Number System (Digits 0 to 7, Base :8)

4) Hexadecimal Number System (Digits 0 to F, Base :16)
                                                     (0 to 9 and)
                                                     (10 as A)
                                                     (11 as B)
                                                     (12 as C)
                                                     (13 as D)
                                                     (14 as E)
                                                     (15 as F)

Now we will learn how to convert one type of number system to another.

Decimal to Binary Number :

to convert a decimal number to a binary number we will divide the decimal number by the base of binary number system (2) and collect the remainders in "bottom to top" order.

Let us understand by an example:

convert (75)10    to   ( )2 .

Now,

we will divide 75 by 2                                        

now storing the remainders in bottom to top order we will get the binary number as:

(1001011 )2

thus,    (75)10  = ( 1001011)2.

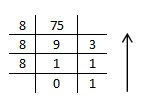
Decimal to Octal Number :

to convert a decimal number to an Octal number we will divide the decimal number by the base of Octal number system (8) and collect the remainders in "bottom to top" order.

Let us understand by an example:

convert (75)10    to   ( )8 .

Now,

we will divide 75 by 8                                                                                          

now storing the remainders in bottom to top order we will get the octal number as:

(113 )8

thus,     (75)10  = ( 113)8.

Decimal to Hexadecimal Number :

to convert a Decimal number to a Hexadecimal number we will divide the decimal number by the base of Hexadecimal number system (16) and collect the remainders in "bottom to top" order.

Let us understand by an example:

convert (75)10    to   ( )16 .

Now,

we will divide 75 by 16                                                    

now storing the remainders in bottom to top order we will get the hexadecimal number as:

(4B )16

thus,     (75)10  = ( 4B)1.

Binary to Decimal Number:

to convert a Binary number to Decimal number multiply the digits of Binary number from right to left direction, i.e. the rightmost digit first and the last digit in the end by 2 raising increasing power starting with 0.

Take an example:

convert (10110)2    to   ( )10

Now,

Thus,   (10110)2   =  (22 )10

Octal to Decimal Number:

to convert an Octal number to Decimal number multiply the digits of Octal number from right to left direction, i.e. the rightmost digit first and the last digit in the end by 8 raising increasing power starting with 0.

Take an example:

convert (74)8    to   ( )10

Now,          

Thus,   (74)8   =  (60 )10

Hexadecimal to Decimal Number:

to convert a Hexadecimal number to Decimal number multiply the digits of Hexadecimal number from right to left direction, i.e. the rightmost digit first and the last digit in the end by 16 raising increasing power starting with 0.

Take an example:

convert (7A2)16    to   ( )10

Now,             

Thus,   (7A2)16   =  ( 935)10

Octal to Binary Number:

There are 2 ways to convert an Octal number to Binary number

     1)  Convert octal number to Decimal number and than convert the decimal to binary number.

     2) Direct conversion

we will do the 2nd method of direct conversion. For this type of conversion we have to convert every individual digit of Octal number to binary equivalent as per the table below and write conversions together from left to right.

       

take an example:

convert (75)8     to   ( )2

Now,  

write the binary equivalent of both 7 and 5 from the table in the order of occurrence in the number from left to right, i.e. first 7 then 5

     

        

 

hence,

            (75)8     =   (111101 )2

If you do not want to learn the table than there is 1 trick to do the same.

convert (75)8     to   ( )2

Since the highest digit of an Octal Number System requires 3 binary bits (7 is 111 in binary) to get stored in binary form, so to convert octal digits we will take 3 digits "4, 2, 1" and write '1' under those digit whose sum makes the octal digit to be converted, otherwise write '0'. For example in the above case to get 7 we have to mark 1 under all 4, 2, 1 as all of them after addition makes 7, while to make 5 we have to mark 1 under only 4 & 1 as they adds to make 5.

as you can see that all 4+2+1 makes 7 thus we have written 1 under all 3 while only 4+1 makes 5 thus 1 is written under 4 & 1 only and 2 is marked as 0 since it is not required to get 5.

so we can write

(75)8     =   (111101 )2

thus conversion is done.

Binary to Octal Number:

There are again 2 ways to convert a binary number to octal. First is to convert it to decimal, then to octal. Second way, which we will do is:

           Make groups of 3 digits from right to left and write their octal digits from the table above. If the leftmost group is left with 1 OR 2 digits then write "0's" to make it a group of 3 digits. Then write the converted digits combined from left to right to make the octal number. Let us understand it with the help of an example.

convert    (1101001011)2     to   ( )8

Make the groups of binary number: 

Now write the digits from left to right order  (1513 )8

Hence,

(1101001011)2     =   (1513 )8

Hexadecimal to Binary Number:

We have 2 ways (same as Octal) to convert a Hexadecimal number to Binary number

     1)  Convert Hexadecimal number to Decimal number and than convert the decimal to binary number.

     2) Direct conversion

we will do the 2nd method of direct conversion. For this type of conversion we have to convert every individual digit of Hexadecimal number to binary equivalent as per the table below and write conversions together from left to right.

take an example:

convert (7AD)16     to   ( )2

Now,  

write the binary equivalent of all 7, A & D from the table in the order of occurrence in the number from left to right, i.e. first 7 then A and then D

hence,

          (7AD)16     =   (011110101101 )2

Here again, if you do not want to learn the table than there is 1 same trick as was in the case of octal number to do the same.

convert   (7AD)16     to   ( )2

Since the highest digit of a Hexadecimal Number System requires 4 binary bits (F is 1111 in binary) to get stored in binary form, so to convert hexadecimal digits we will take 4 digits "8, 4, 2, 1" and write '1' under those digit whose sum makes the octal digit to be converted, otherwise write '0'. For example in the above case to get 7 we have to mark 1 under  4, 2, 1 and '0' uder '8' as only "4, 2, & 1" adds to make 7, while to make 'A' we have to mark 1 under  8 & 2 (rest 4 & 1 as 0) as they adds to make A.

as you can see that 4+2+1 makes 7 thus we have written 1 under them while 8+2 makes 'A' so 8 & 2 are "1" and "2 & 1" are "0". Similarly 8+4+1 makes 'D' so 8, 4 & 1 are "1" and "2" is "0".

hence, we can write.

                                       (7AD)16     =   (011110101101 )2

thus conversion is done.

Binary to Hexadecimal Number:

There are again 2 ways to convert a binary number to hexadecimal. First is to convert it to decimal, then to hexadecimal. Second way, which we will do is:

           Make groups of 4 digits from right to left and write their hexadecimal digits from the table above. If the leftmost group is left with 1, 2 OR 3 digits then write "0's" to make it a group of 4 digits. Then write the converted digits combined from left to right to make the hexadecimal number. Let us understand it with the help of an example.

convert    (1101001011)2     to   ( )16

Make the groups of binary number: 

Now write the digits from left to right order  (34B )16

Hence,

(1101001011)2     =   (34B)16